Hello!
I’m trying to extract metrics for MWF analysis on spinal cord images and I wanted to get clarification on this particular output from the sct_extract_metric command: Total fractional volume of the label (in number of voxels)
I couldn’t find any documentation with regard to what this metric means in relation to my MWF images, so I’m hoping someone can help!
My script is as follows (using activate_sct327.sh)
for y in {0…2…2}; do
for i in “${participantList[@]}”; do
sct_extract_metric -i /Data/${i}/Yr${y}/${i}_Yr${y}_MWF.nii.gz -l 50:55 -f /Data/${i}/Yr${y}/reg_mwf/warped_template/atlas -o /Data/JW_Yr${y}_metric_values.xls -overwrite 0 -z 3:12;
done
done
Thanks in advance!
Jessica Wang (she/her)
MD 2023 Candidate | UBC Faculty of Medicine
Hello Jessica,
Thank you for reaching out. The Total fractional volume of the label corresponds to the number of voxels that are used to compute the statistics. For example, if you extract metrics using the spinal cord segmentation on a slice-by-slice basis (ie: -perslice 1), the number of voxels with value=1 (ie corresponding to the spinal cord) will be, let’s say, 80. So, the mean and standard deviation will be computed out of 80 voxels.
Now, if you compute the same thing, but over the enter volume (ie: -perslice 0), the Total fractional volume of the label will be much bigger. Let’s say, if you have 10 slices, it will be about 800.
If you use non-binary masks (such as the ones present in under label/atlas), the fractional volume means the same thing, except it can be in float. E.g., instead of 80, it will be 79.6. Soft masks are better in that it can take into account partial volume information.
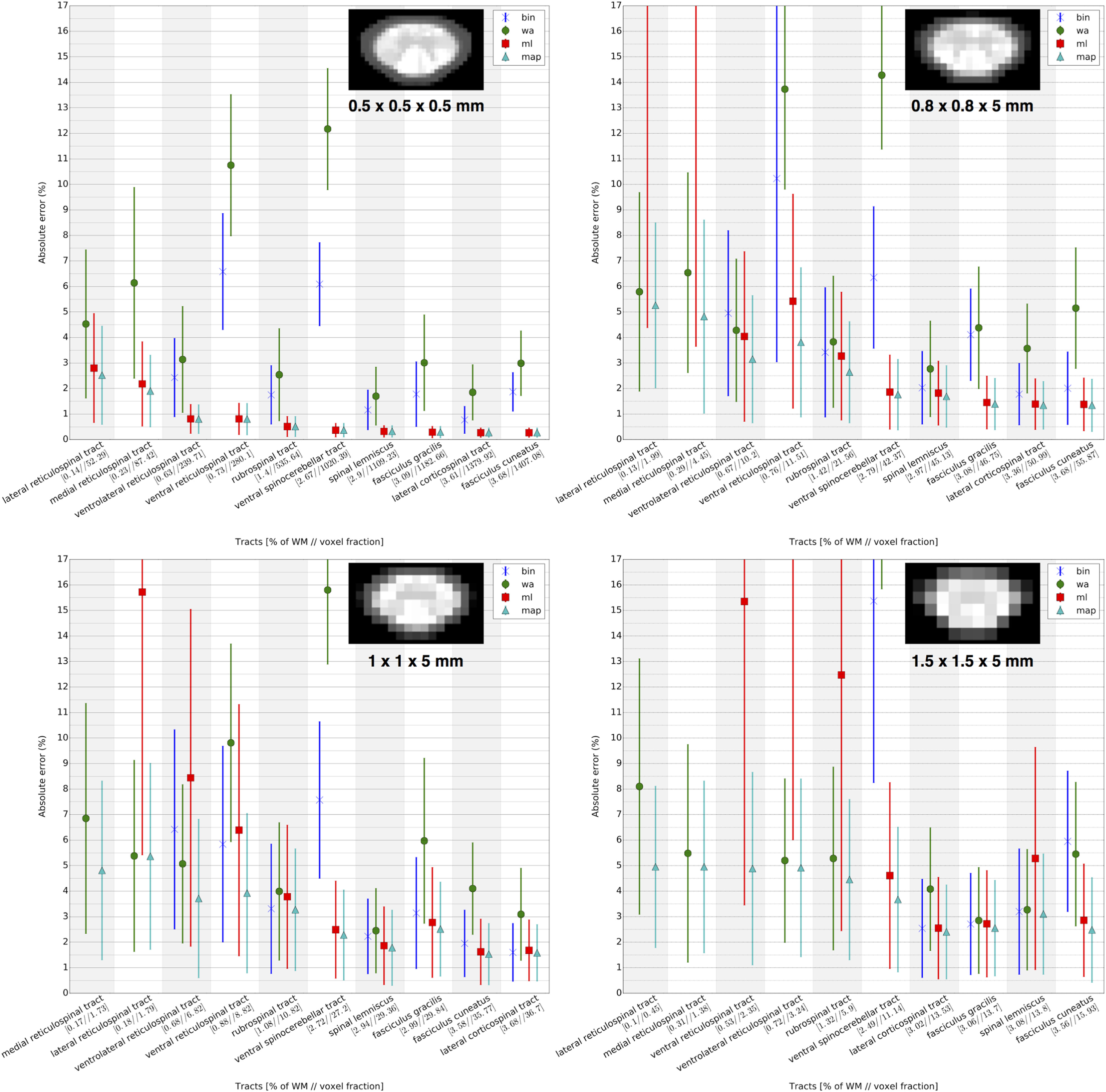
I encourage you to read thoroughly the article by Levy et al. Neuroimage 2015, as well as from De Leener et al. Neuroimage 2017 which discuss the concept of fractional volume, and its implication with respect to the precision and accuracy of metric extraction. See notably Fig11 from De Leener et al.:
Simulation results comparing the accuracy and precision of metric extraction methods at various resolutions. Metric extraction methods are: averaging within binary mask (bin), weighted-averaging within probabilistic mask (wa), maximum likelihood estimation (ml) and maximum a posteriori estimation (map) (Lévy et al., 2015). The abscissa shows different left tracts, ordered by their volume fraction occupied within the white matter. The volume fraction of a given tract (expressed here in percentage) represents the number of voxels of this tract divided by the number of voxels in the white matter (each voxel being represented by its partial volume information). An image of a randomly-generated synthetic phantom is shown at each resolution. The ordinates show the mean and STD of the absolute error (in percentage of the true value). Note that for very low volume fractions, the bin method is not represented because the tract is too small to pass the 0.5 threshold.
Julien